Comparison of Nonlinear Functions using Partial Growth Data at Different Lengths of Growth Period in Awassi Lambs

Nihat Tekel1, Seyrani Koncagül2, İlkay Baritci1, Halit Deniz Şireli1, Muhittin Tutkun1, Ecevit Eyduran3 and Mohammad Masood Tariq4*

1Department of Animal Science, Faculty of Agriculture, Dicle University, 21280 Diyarbakır, Turkey

2Department of Animal Science, Faculty of Agriculture, Ankara University, 06210 Ankara, Turkey

3Department of Business Administration, Quantitative Methods, Faculty of Economics and Administrative Sciences, Iğdır University, Iğdır, Turkey.

4Center for Advanced Studies in Vaccinology and Biotechnology, University of Balochistan, Quetta, Pakistan

ABSTRACT

The aim of this study was to comparatively evaluate some nonlinear functions i.e. Brody, Negative Exponential and Bertalanffy in order to describe the growth of Awassi male lambs (n=120) at the age of 10 months. The coefficient of determination values estimated for Brody, Negative Exponential and Bertalanffy models were 0.9523, 0.6094, and 0.9428 R2 for the first-time interval (0-90 days of age), 0.9866, 0.9743 and 0.9797 R2 for the second time interval (0-180 days of age) and 0.9924, 0.9853 and 0.9902 R2 for the third time interval (0-300 days of age), respectively. Pearson correlation coefficients between the observed and predicted weight values of the Awassi lambs were found as 0.9417, 0.9255 and 0.9203 for 0-90 days of age, 0.9741, 0.9501 and 0.9634 for 0-180 days of age and 0.9824, 0.9765 and 0.9790, for 0-300 days of age, respectively. Brody, Negative Exponential and Bertalanffy models were found to be useful models to describe the growth of Awassi lambs raised in Turkey. In conclusion, it could be suggested that the nonlinear functions might allow breeders to achieve remarkable information in practice in terms of determining managerial problems, slaughtering age, ideal feed amounts, and the studied breed’s growth standards.

Article Information

Received 04 February 2019

Revised 28 July 2019

Accepted 11 September 2019

Available online 11 December 2020

Authors’ Contribution

NT performed experiments and wrote this manuscript. İB, HDS and MT performed experiments. SK, EE and MMT analyzed the data and edited the manuscript,

Key words

Awassi, Brody, Negative exponential, Bertalanffy, Growth

DOI: https://dx.doi.org/10.17582/journal.pjz/20190204150214

* Corresponding author: [email protected]

0030-9923/2021/0001-0153 $ 9.00/0

Copyright 2021 Zoological Society of Pakistan

INTRODUCTION

Growth is known to be a fundamental property of biological systems at the level of populations, individual animals and plants, and within organisms. A graphical representation of the changes in weight over time is expressed as a growth curve (Bathaei and Leroy, 1998; Efe, 1990, Topal et al., 2004; Akbas et al., 1999; Kocabas et al., 1997).

Nonlinear growth functions, which allow ones to decide managerial problems, slaughtering age, ideal feed amounts, and the studied breed’s growth standards for selection schemes, are mathematical expressions of the growth limited by genotype and non-genetic factors. In addition, the nonlinear functions allow breeders to obtain describe maturate weight and maturing rate owing to economical magnitude in sheep breeding. For selection programs, it is imperative to estimate biological parameters of the nonlinear functions and genetic correlations between the parameters.

Many studies have been conducted by mechanical models using time series and stochastic differential equations in order to model the growth processes in the living. Nonlinear growth functions (linear or non-linear) employed to mathematically describe the growth depend on the animal species, environmental condition, the studied character and the growth pattern (Draper and Smith, 1981). In literature, Logistics, Gompertz, Brody, Negative Exponents, Richards, Bertalanffy and Monomolecular nonlinear functions are growth curve models known well (Finney, 1978).

The actual live weights of living organism feeding by balanced manner show characteristic growth curve in their life time when it is considered as a function according to age. This curve has a “Sigmoid” pattern which is similar to the S letter (Lawrence and Fowler, 2002).

In sheep, growth curves are usually used for predicting the increase in live weight and mature-fresh- live weight. Many researchers have conducted different nonlinear functions to capture the best fitted one among the nonlinear functions to describe sigmoidal relationship between body weight-age in farm animals. Nasholm and Dannell (1990) used the Negative Exponential growth curve model in Swedish Fine wool Landrace sheep, Bilgin et al. (2004) comparatively examined Brody, Gompertz, Logistic and Bertalanffy, Richards Nonlinear function for describing the growth of the Turkish Awassi and Morkaraman sheep, Bathaei and Leroy (1996; 1998) employed the Brody model in fat-tailed Mehreban sheep, Topal et al. (2004) implemented Brody, Gompertz, Logistic and Bertalanffy in describing the growth of Turkish Awassi and Morkaraman sheep, Malhado et al. (2009) have determined that Bertalanffy, Brody and Logistic models were suitable to describe the growth of crossbred lambs obtained by crossing Dorper sheep with Morado Nova, Rabo Largo and Santa Ines sheep. Kucuk and Eyduran (2009) fitted Monomolecular, Logistic and Gompertz nonlinear functions to body weight-age data for Akkaraman and German Blackheaded Mutton x Akkaraman B1 crosbreed lambs. Tariq et al. (2013) studied the growth of Mengali sheep, Pakistan by means of Gompertz, Logistic, Bertalanffy, Richards, Weibull and Morgan-Mercer-Flodin (MMF) nonlinear functions for the time interval, 0-365 days of age.

When growth curve models are fitted to estimate asymptotic body weight by using partial growth data which were not reached the asymptotic weight, there is no guarantee that the growth models describe the data adequately (Brisbin et al., 1987). Therefore, the present study was undertaken to reveal sensitivity of Brody, Logistics and Negative Exponential growth functions to data reduction for describing growth curves and predicting future growth trajectory of Turkish Awassi ram lambs. To achieve this aim, partial growth data used until the time when maximum body weight had been reached.

 

MATERIALS AND METHODS

In all Awassi lambs (n=120) born in the lambing season of Ceylanpınar State Farm were used in the experiment. These lambs were grown under regular care and feeding conditions at the sheep farm (36°83’N, 39°65’E).

Biological fit of non-linear models of Brody, Negative Exponential and Bertalanffy (Formula of those models were given Table I) to growth performances of Awassi lambs using period (obtained from data of live weight from birth to 10 months old) were investigated. Predictions of non-linear models were made using iterative Levenberg-Marquardt method.

 

Table I. Growth models and their formulation and their fit to growth data of lambs.

Models	Formulation
Bertalanffy	Y=A*(1-B*exp(-k*x))3
Brody	Y=A*(1-B*exp(-k*x))
Negative Exponential	Y=A-A*exp(-k*x)

 

Since consecutive or repeated measurements are usually auto correlated, the growth models were fitted to individual lambs to remove possible bias in the statistical inference on the growth parameters. Each growth model performed three times for every individual lambs; first analyses were carried out using data taken from day 0 to day 90 (BW0-90), second analyses were conducted by using the growth data taken from day 0 to day 180 (BW0-180) and the third analyses were performed by using the growth data taken from day 0 to day 300 (BW0-300). When the statistical analyses were completed, the model parameters were used to predict the growth data from 0 to 300 days and Pearson correlation coefficients between the observed and the predicted body weights were estimated. Models were compared using coefficient of correlation (R2) to show how well a model fits the data, Residual Standard Deviation (RSD) which measures the error in absolute terms (Congleton and Everett, 1980; Guo and Swalve, 1995) without recognizing its variation through the growth trajectory and correlation between the observed and the estimated body weights (r) which quantifies the degree of association between real and estimated growth curves. Calculations were carried out with non-linear regression option in the SPSS (version 15.0) statistical software package program with Levenberg-Marquart estimation method. Priors were obtained from the previous studies in the literature (Anthony et al., 1986). Convergence criterion was the relative reduction between successive residual sums of squares and was set to 1.0E-08.

The RSD and R2 formulas were given below:

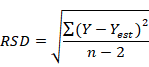
Where:

Residual=(Y−Yest)

Y=Observed value

Yest=Estimated or projected value

n=data points in population

Where:

SSE=Sum of square

SST=Total sum of square

The parameters A, b, k, and x refer the predicted mature live weight, folding point of growth, growth rate and age (the time from birth to10 months) respectively.

 

RESULTS

In this study, the changes of live weights of Turkish Awassi male lambs according to different time intervals (0-90 days, 0-180 days and 0-300 days of age) were examined by using Brody, Negative Exponential and Bertalanffy models. The parameters obtained from the results are given in Table II with Determination Coefficients (R2) and Residual Standard Deviation (RSD).

 

Table II. Model parameters, estimated coefficients of determination, and residual standard deviations for Bertalanffy, Brody, and negative exponential non-linear regression models in Turkish Awassi ram lambs.

Model	BW0-90	BW0-180	BW0-300
Bertalanffy
A	274.3±56.95	35.8±0.47	39.4±0.62
B	0.7±0.02	0.6±0.01	0.6±0.01
K	0.01±0.001	0.02±0.001	0.01±0.00
R2	0.9523	0.9866	0.9924
RSD	2.6±0.17	2.2±0.12	2.1±0.10
Brody
A	123.9±22.04	54.4±3.60	47.4±3.55
B	0.90±0.008	0.88±0.052	0.98±0.029
K	0.002±0.0003	0.01±0.000	0.02±0.014
R2	0.6094	0.9743	0.9853
RSD	9.4±0.44	2.9±0.23	2.7±0.20
Negative exponential
A	215.1±30.62	42.4±1.12	42.4±1.17
K	0.01±0.001	0.01±0.0003	0.01±0.0002
R2	0.9428	0.9797	0.9902
RSD	3.8±0.14	3.0±0.10	2.8±0.09

 

BW0-j: Only data from day 0 to day j included in the analyses; R2: Estimated coefficients of determination; RSD: Residual standard deviations.

 

As part of describing the growth data of the lambs, the R2 values obtained for the Brody, Negative Exponential and Bertalanffy were found 0.9523, 0.6094, and 0.9428 for the first-time interval (0-90 days of age). Corresponding values were 0.9866, 0.9743, 0.9797 for the second time interval (0-180 days of age) and 0.9924, 0.9853 and, 0.9902 for the third time interval (0-300 days of age) (Table II).

The present R2 values were found as 0.9523, 0.6094 and 0.9428, respectively for the first-time interval, 0-90 days of age for Brody, Negative Exponential and Bertalanffy nonlinear functions. Corresponding R2 values were estimated as 0.9866, 0.9743 and 0.9797 for the second time interval, 0-180 days of age and 0.9924, 0.9853 and 0.9902 for the third time interval, 0-300 days of age respectively. R2 values of applied models are 0-90, 0-180 and 0-300 days-old growth data were high but only R2 value obtained by applying Brody model to 0-90 days-old growth data (0.6094) was low.

The present standard deviations were estimated for the first-time interval, 0-90 days of age as 2.6±0.17, 9.4±0.44 and 3.8±0.14 for the second time interval, 0-180 days of age as 2.2±0.12, 2.9±0.23 and 3.0±0.10 for the third time interval, 0-300 days of age as 2.1±0.10, 2.7±0.20 and 2.8±0.09 respectively (Table II).

 

Table III. Correlation between the observed and predicted body weights for Bertalanffy, Brody, and negative exponential non-linear regression models in Turkish Awassi ram lambs.

Model	BW0-90	BW0-180	BW0-300
Bertalanffy
BW0-90	0.9417		0.9502
BW0-180		0.9741	0.9781
BW0-300			0.9824
Brody
BW0-90	0.9255		0.9515
BW0-180		0.9501	0.9603
BW0-300			0.9765
Negative exponential
BW0-90	0.9203		0.9552
BW0-180		0.9634	0.9745
BW0-300			0.9790

 

BW0-j: only data from day 0 to day j included in the analyses, then data from day 0 to day 300 were predicted; r: Correlation between the observed and predicted body weights.

 

Bertalanffy model produced the lowest standard deviation (Table II). The Bertalanffy nonlinear function has been found to be the most adequate model describing the growth of male Awassi lambs.

The A values expressing estimated adult weight for the first-time interval, the 0-90 days of age was found as 274.3±56.95, 123.9±22.04 and 215.1±30.62 for Brody, Negative Exponential and Bertalanffy nonlinear functions. For the second time interval, 0-180 days of age, corresponding values were estimated as 35.8±0.47, 54.4±3.60 and 42.4±1.12, and for the last time interval, 0-300 days of age as 39.4±0.62, 47.4±3.55 and 42.4±1.17 respectively. For the second time interval, our results were almost in line with those reported by Kucuk and Eyduran (2009).

The growth curves were plotted actual weight values and weight values predicted by the studied nonlinear functions in order to describe the growth of Awassi lambs of the models used in the research and their adequacy to predict mature live weights. After obtaining the biological parameters related to each of the evaluated nonlinear functions, weight values at 90, 180 and 300 days of age for each lamb were estimated by means of these parameters. Growth curves were plotted with the predicted value and actual BW values (Figs. 1, 2 and 3). Then, Pearson correlation coefficients between predicted and actual values were estimated (Table III).

The high correlation coefficients between actual and predicted weight values for Bertalanffy, Brody and Negative Exponential models were noted. When Figures 1, 2, 3 and Table III are taken into consideration together, it was understood that the ability of each function to predict 300 days growth using 90, 180, and 300 days actual data increase with the estimated age close to real age data.

 

 

As a matter of fact, when looking at the shapes of the growth curves, it is seen that the curves plotted with actual values are more similar to the estimated 180 days used from the 300 days data. The present estimates obtained from 180-days data are more similar to those plotted with actual values compared to 90-days of age. Likewise, Pearson correlations between live weights increase as the estimated age and actual age approaches each other (from 90 days to 300 days of age).

 

Correlation between live weights increases as the estimated and actual age close to each other (from 90 days old to 300 days old) by using the same model. Based on the correlation coefficients between growth curves and actual predictive values, it can be assumed that the Bertalanffy, Brody and Negative Exponential models used in this study have sufficient sensitivity to describe the growth at a level sufficient in Awassi lambs.

 

DISCUSSION

Determination of Coefficients (R2) and Residual Standard Deviation (RSD) were used as goodness of fit criteria in measuring the suitability of the nonlinear growth functions applied for biologically identifying the sigmoidal relationship between body weight and age was also studied by various previous researchers as also in the present study (Keskin et al., 2009; Topal et al., 2004; Malhado et al., 2009).

Results showed that R2 values obtained for different three-time intervals i.e. 0-90, 0-180 and 0-300 days of age were high but only R2 value obtained by applying Brody model for 0-90 days-old growth data (0.6094) was found low. Similarly, Topal et al. (2004) applied the Bertalanffy, Brody and Logistic models in Awassi and Morkaraman lambs. Malhado et al. (2009) have used the Bertalanffy, Brody and Logistic nonlinear growth functions for describing body weight-age relationship of the lambs obtained by crossing Dorper sheep with Morado Nova, Rabo Largo and Santa Ines sheep. The negative Exponential, Bertalanffy and Brody models were determined to be sufficient in order to explain the sigmoidal relationship between live weight and age of lambs.

The lowest standard deviation for Bertalanffy model in this study shows similarity with those reported by Topal et al. (2004) who used the Brody, Gompertz, Logistic and Bertalanffy models describe the live weight-age data of Turkish Awassi and Morkaraman lambs and reported that the Bertalanffy model produced a smaller standard deviation. Malhado et al. (2009) applied Bertalanffy, Brody, Gompertz, Logistic and Richards models to live weight-age data and obtained the smallest standard deviation from Gompertz and Logistic models. The lowest standard deviations in this study were possible with the Bertalanffy model. According to standard deviations, Bertalanffy models have been determined to be the best fitted model for describing the growth of male Awassi lambs. In the agreement with our results, Kucuk and Eyduran (2009) found that monomolecular was the best nonlinear function in describing the growth of Akkaraman (0.99935 R2) and German Blackheaded Mutton x Akkaraman B1 crosbreed (0.99869 R2) lambs for the time interval 0-180 days of age. In describing the growth of Mengali sheep, Tariq et al. (2013) reported that Morgan-Mercer-Flodin (MMF) gave the best fit among Gompertz, Logistic, Bertalanffy, Richards, Weibull and Morgan-Mercer-Flodin (MMF) nonlinear functions for the time interval, 0-365 days of age.

Topal et al. (2004) determined “A” growth parameters for the Brody, Gompertz, Logistic and Bertalanffy models in the Turkish Awassi sheep as 47.0±1.89, 40.6±1.00, 38.9±0.93 and 41.7±1.10, respectively. In this study, the A values regarding present nonlinear functions s were found to be consistent with the reports of Topal et al. (2004), except for the growth period of 0-90 days. Tariq et al. (2013) reported that A parameters for Gompertz (36.966), Logistic (35.0583), Bertalanffy (44.2992), Richards (44.0385), Weibull (43.8946) and Morgan-Mercer-Flodin (57.0618) nonlinear functions for the time interval, 0-365 days of age. For Gompertz, Brody, Bertalanffy, Monomolecular, Logistic, Richards, and Weibull models, Waheed et al. (2016) found it as 28.2, 33.1, 28.9, 33.1, 27.1, 28.2 and 28.0 for the time interval, 0-365 days of age in Thalli sheep. The wide variation may be ascribed to genetic and non-genetic factors, the time interval, nonlinear functions etc.

 

CONCLUSION

Results indicated that the nonlinear growth functions handled here permit breeders to accomplish remarkable information in order to make a proper decision on finding out managerial problems, slaughtering age, ideal feed amounts, and the investigated breed’s growth standards.

 

Statement of conflict of interest

Authors have declared no conflict of interest.

 

REFERENCES

Akbas, Y., Taskin, E. and Demiroren, E., 1999. Comparison of several models to fit the growth curves of Kıvırcık and Daglıç male lambs. Turkish J. Vet. Anim. Sci., 23: 537-544.

Anthony, N.B., Nestor, K.E. and Bacon, W.L., 1986. Growth curves of Japanese quail as modified by divergent selection for 4-week body weight. Poult. Sci., 65: 1825–1833. https://doi.org/10.3382/ps.0651825

Bathaei, S.S. and Leroy, P.L. 1996. Growth and mature weight of Mehraban Iranian fat-tailed sheep. mall Rumin. Res., 22: 155-162.

Bathaei, S.S. and Leroy, P.L., 1998. Genetic and phenotypic aspects of the growth curve characteristics in Mehraban Iranian fat-tailed sheep. Small Rumin. Res., 29: pp. 261-269. https://doi.org/10.1016/S0921-4488(97)00142-9

Bilgin, O.C., Esenbuga, N., Macit, M. and Karaoglu, M., 2004. Growth curve characteristics in Awassi and Morkaraman sheep, Part I: Comparison of nonlinear functions. Wool Technol. Sheep Breed., 52: 1-7. https://doi.org/10.1080/09712119.2004.9706496

Brisbin, I.L., Collins, J.R.C.T., White, G.C. and McCallum, D.A., 1987. A New paradigm for the analysis and interpretation of growth data: The shape of things to come. Auk, 104: 552-554. https://doi.org/10.2307/4087567

Congleton, W.R. and Jr, Everett, R.W., 1980. Application of the incomplete gamma function to predict cumulative milk production. J. Dairy Sci., 63: 109-119. https://doi.org/10.3168/jds.S0022-0302(80)82895-5

Draper, N.R. and Shimth, H., 1981. Applied regression analysis. John Wiley and Sons. Inc., Chichester.

Efe, E., 1990. Growth curves, PhD thesis. Çukurova University, Graduate School of Natural and Applied Science, Adana.

Finney, D.J., 1978. Growth curves. Their nature uses and estimation. In: Patterns of growth and development in cattle Martinus-Nijhaf (ed. He De Boer and J. Martin). The Hague, pp. 658-672. https://doi.org/10.1007/978-94-009-9756-1_42

Guo, Z. and Swalve, H.H., 1995. Modelling of the lactation curve as a sub-model in the evaluation of test day records. Interbull. Bull., 11: 22-25.

Iqbal, F., Tariq, M.M., Eyduran, E., Huma, Z., Waheed, A., Abbas, F., Ali, M., Rashid, N., Rafeeq, M., Asadullah and Mustafa, Z., 2019. Fitting nonlinear growth models on weight in Mengali sheep through Bayesian inference. Pakistan J. Zool., 51:459-466. http://dx.doi.org/10.17582/journal.pjz/2019.51.2.459.466

Keskin, İ., Dağ, B., Sarıyel, V. and Gökmen, M., 2009. Estimation of growth curve parameters in Konya Merino Sheep. S. Afri. J. Anim. Sci., 39: 163-168. https://doi.org/10.4314/sajas.v39i2.44390

Kocabaş, Z., Kesici, T. and Eliçin, A., 1997. Growth curves in Akkaraman, Awassi x Akkaraman and Malya x Akkaraman lambs. Turk. J. Vet. Anim. Sci., 21: 267-275.

Kucuk, M. and Eyduran, E., 2009. The determination of the best growth model for Akkaraman and German blackheaded mutton x Akkaraman B1 crosbreed lambs. Bulgarian J. agric. Sci., 15: 90-92.

Lawrence, T.J.L. and Fowler, V.R., 2002. Growth of farm animals. CABI Publishing, CAB International Wallingford Oxon OX10 8DE, UK.

Malhado, C.H.M., Carneiro, P.L.S., Affonso, P..RA.M., Souza, Jr A.A.O. and Sarmento, J.L.R., 2009. Growth curves in Dorper sheep crossed with the local Brazilian breeds, Morada Nova, Rabo Largo and Santa Ines. Small Rumin, Res., 84: 16-21. https://doi.org/10.1016/j.smallrumres.2009.04.006

Nasholm, A. and Danell, O., 1990. Growth and mature weight of Swedish Fine Wool Landrace ewes. I. Growth curves and estimation of individual mature weight. Acta Ag. Scan., 40: 71-81. https://doi.org/10.1080/00015129009438549

SPSS, 2006. SPSS for windows release. 15.0 SPSS Inc., Chicago.

Tariq, M.M., Iqbal, F., Eyduran, E., Bajwa, M.A., Huma, Z.E. and Waheed, A., 2013. Comparison of non-linear functions to describe the growth in Mengali sheep breed of Balochistan. Pakistan J. Zool., 45: 661-665.

Topal, M., Özdemir, M., Aksakal, V., Yıldız, N. and Doğru, U., 2004. Determination of the Best Nonlinear Function in order to Estimate Growth in Morkaraman and Awassi Lambs. Small Rumin. Res., 55: 229-232. https://doi.org/10.1016/j.smallrumres.2004.01.007

Waheed, A., Eyduran, E., Tariq, M.M., Ahmad, S., Hameed, T. and Bukhari, F.A., 2016. Comparison of the non-linear models defining the growth of Thalli sheep under desert conditions. Pakistan J. Zool., 48: 423-426.