Description of Factors Influencing Final Fattening Weight in Domestic Beef Cattle Breeds through Mars Algorithm
Description of Factors Influencing Final Fattening Weight in Domestic Beef Cattle Breeds through Mars Algorithm
Yakup Erdal Ertürk
Department of Agricultural Economics, Agricultural Faculty, Iğdır University, Iğdır, Turkey
ABSTRACT
This paper deals with describing several influential factors that have significant impact on final fattening weight (FFW) as an output variable at domestic beef cattle enterprises from the Eastern part of Turkey. Multivariate adaptive regression splines (MARS) as a non-parametric analysis technique was preferred in the description of the influential factors and their interaction effects for each gender. Some probable factors such as age, province, education level, experience, social security, lands, and the reason at performing animal production were recorded on breeders. Also, first fattening weight and fattening period of the beef cattle were recorded. It was determined that predictive models based upon MARS algorithm explained virtually all of variability in the final fattening weight (FFW) for each gender when model assessment criteria (viz. R2, SDRATIO, GCV and Pearson correlation coefficient between real and estimated scores in the final fattening weight) in the current study were considered. SDRATIO estimates of the MARS models for male and female domestic beef cattle were close to 0.05. The estimated FFW scores were correlated almost at the highest level with the observed FFW scores for each gender (r~1.000, P<2.2 e-16). The R2 estimates were also the closest to unity for each gender. The results showed that MARS is a recommendable model in description of influential factors for subsequent comparable studies.
Article Information
Received 07 November 2017
Revised 19 December 2017
Accepted 02 January 2018
Available online 03 August 2018
Key words
Fattening performance, Native beef cattle, MARS, Final fattening weight, Data mining.
DOI: http://dx.doi.org/10.17582/journal.pjz/2018.50.5.1731.1737
* Corresponding author: [email protected];
0030-9923/2018/0005-1731 $ 9.00/0
Copyright 2018 Zoological Society of Pakistan
Introduction
Beef cattle are one of the most essential red meat sources that fulfill basic nutritional requirements of human population in the world. Beef cattle production as a cardinal segment of animal production sector is of great significance in ensuring better rural development in Turkey (Demircan et al., 2007) where small-scale enterprises rearing animals through traditional methods are widespread (Tutkun, 2017). Domestic, cultural and crossbred beef cattle have been reared in various regions of Turkey, but domestic beef cattle rearing is a prominent consideration not only to conserve indigenous gene sources therein but also to have high adaptability against harsh climate conditions. When viewed from this aspect, domestic cattle are important animal materials in mating systems in order to produce better crossbred offspring in improving weight. Within this framework, the final fattening weight (FFW) is one of the most prime quantitative traits, economically in domestic beef cattle rearing and it may be influenced by many factors viz. breed, age, gender, the first weight before fattening, fattening period, management and feeding situations etc. Additionally, some factors regarding beef cattle breeders; such as age, the level of education, and experience of the breeders are a useful selection to be taken into account in the explanation of total variability in FFW of the beef cattle and it is also of vital importance to take advantage of powerful statistical techniques in an accurate assignation of factors affecting FFW. In this respect, data mining applications are very impactful.
Previously, some authors have highlighted past, current and successive situations of beef cattle production in South of Africa (Marle, 1974) and Italy (Cozzi, 2007). There are a high number of previous researches on FFW in beef cattle production. Generally speaking, animal material, feed, and the remaining expenses (labor, loan interest and veterinary expenses) are indispensable fattening input costs (Tutkun, 2017). Sarma et al. (2014) investigated the profitability of beef cattle fattening enterprises in Bangladesh by obtaining information on socio-economic and beef fattening predictors. Abo Elfadl et al. (2015) made an evaluation for revealing factors that can be influential on profitability and productivity of beef fattening enterprises in Egypt. Ahmed et al. (2010) aimed to find out some factors that affected fattening performances at small-scale enterprises in Bangladesh rural conditions. Aydin et al. (2014) evaluated performances of cattle fattening enterprises through data envelopment analysis method. Koknaroglu et al. (2005) determined factors influencing performance and profitability of the beef cattle in USA. Muižniece and Kairiša (2016) studied fattening performances of Blonde d’Aquitaine, Hereford, Simmental and crossbred bulls reared in organic farming system in Latvia, and determined the effect of breed, age, and live weight before fattening on fattening performances. Aytekin et al. (2017) estimated FFW from fattening period and morphological traits from 103 young bulls of domestic, crossbred and exotic breeds by means of MARS data mining application and examined the effect of genotype and fattening period on FFW.
Abo Elfadl et al. (2015) emphasized that it is necessary that economic, biological and social factors should be examined jointly in order to obtain maximum production level of beef cattle. In the description of the most significant factors, more reliable records are still scarce and the powerful and sophistical statistical approaches has not been studied for more successful comments and evaluations. In this respect, MARS can present a more powerful approach for analysts compared with the other data mining applications such as C5.0, CART (Kowalchuk et al., 2017), CHAID (Akin et al., 2017a, b, c, d), Exhaustive CHAID (Ali et al., 2015) etc. Therefore, this paper aimed at describing several prominent factors influencing final fattening weight (FFW) as a response quantitative trait at domestic beef cattle enterprises in the Eastern part of Turkey via multivariate adaptive regression splines (MARS) data mining approach.
Materials and methods
Data collection and sampling
A questionnaire was applied to describe factors affecting the final fattening weight (FFW) per enterprise for indigenous beef cattle on 101 beef cattle enterprises in the Eastern Anatolia provinces of Erzurum, Igdir, Kars and Agri in Turkey. Fifty one enterprises were analyzed for native male beef cattle. For native female beef cattle, fifty enterprises were evaluated in the study.
Variable structure
The FFW per enterprise was accepted as a target trait. Several predictors evaluated here were province (Erzurum, Igdir, Kars and Agri), Farmer age (year), educational degree (illiterate, primary school, secondary school, high school, and college), social security (available and unavailable), experience of farmer in animal production (year), farmer`s irrigated land (da), farmer`s dry land (da)farmer`s pasturage land (da), the first weight before fattening (kg), and fattening period (day).
Statistical Analysis
Multivariate Adaptive Regression Splines (MARS) also known as a-non parametric regression approach was implemented to develop a beneficial prediction model that can reveal interaction effects of important predictors in the characterization of the significant factors on FLW as an output variable for each gender.
The MARS data mining algorithm implemented here is shown in the following equation:
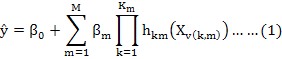
Where, ŷ is the predicted value of the response variable, β0 is a constant, hkm(Xv(k, m)) is the basis function, in which v (k, m) is an index of the predictor employed in the mth component of the kth product, Km is the parameter limiting the order of interaction.
The maximum number of basis functions in the current analysis was 100 and the two-order interactions were used. After building the most complex MARS model, the basis functions that did not contribute much to the quality of the model performance were eliminated in the process of the so-called pruning based on the following generalized cross-validation error (GCV) (Kornacki and Ćwik, 2005):

Where, n is the number of training cases, yi is the observed value of a response variable, yip is the predicted value of a dependent variable and M (λ) is a penalty function for the complexity of the model containing λ terms.
Formulas of the model evaluation criteria for estimating their predictive performance of the MARS algorithms are given below:
1. Coefficient of determination
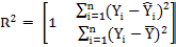
2. Standard Deviation Ratio

3. Pearson correlation coefficient between actual and predicted values in FFW (Kovalchuk et al., 2018).
Where, Yi is the actual or observed FFW (kg) value of ith enterprise, Ŷi is the predicted FFW of ith enterprise, Ῡ is the average of the FFW values of enterprise, ɛi is the residual value of ith enterprise, έi is the average of the residual values, k is the number of terms in the MARS model, and n is total enterprise number. The residual value of each enterprise is expressed as ɛi=Yi – Ŷi.
The MARS model with the smallest GCV, SDRATIO and the highest coefficient of determination (R2) and Pearson coefficient (r) between observed and predicted values in the final fattening live weight was accepted as the best one. All the statistical evaluations were performed through the package `earth` of R software.
Results and discussion
Male native cattle breeds
The fundamental aim of the MARS application is to determine a prediction model producing the smallest GCV estimate. Primarily, MARS model is obtained for the smallest GCV, and the results of MARS algorithm for male native breeds are given in Table I. Model goodness of fit criteria (0.9963 R2 and 0.0514 SDRATIO) showed the highest predictive accuracy of the model structured based on MARS algorithm. Also, Pearson coefficient of 0.9981 indicated a perfect agreement between the observed and the fitted FFW scores for MARS predictive modeling (t = 114.35, df = 49, p-value < 2.2e-16). Several earlier authors acclaimed that SDRATIO value should be lower than 0.10 for very high predictive accuracy of the fitted models. According to the current SDRATIO estimate, the MARS model ensured a very predictive accuracy for native male cattle. Thus, reliable comments could be made as a result of high predictive performance in MARS modeling. The current MARS model goodness of fit criteria results was almost in accordance with those found by Aytekin et al. (2017), who obtained R2 =0.9717, SDRATIO= 0.168 and r=0.986 for MARS model in the same trait of young bulls. Thus, it was determined that MARS algorithm produced more informative results, and the models that have a high predictive accuracy.
Initially, an increase of 53.810503 kg in FFW is expected when SOCSEC situations of enterprises were unavailable, as seen in the second term of Table I. It was determined that the effect of SOCSEC unavailable on FFW could vary based on EFAP and FIRSTLIVEWEIGHT as also understood from 18th to 20th terms (Table I). When SOCSEC of the enterprises were unavailable, the 19th term SOCSEC_unavailable*max(0, EFAP-25) with the coefficient of 213.957838 increased FFW for EFAP > 25 years. As also understood from interaction terms in Table I, it is clear that experience of the farmers in animal husbandry could affect FFW, depending upon influential factors i.e. province, SOCSEC, APAP, ILF, and FATPERIOD.
Table I.- Results of the MARS algorithm for male native beef cattle.
|
Basis functions |
Coefficients |
|
Intercept SOCSEC_ unavailable APAP_trade max(0, 20- EFAP) max(0, EFAP -20) max(0, EFAP -25) max(0, 10- PF) max(0, PF -10) max(0, 200- FIRSTLIVEWEIGHT) max(0,FIRSTLIVEWEIGHT -200) Province_IGDIR* max(0, EFAP -20) Province_IGDIR* max(0, FIRSTLIVEWEIGHT-200) Province_KARS * max(0, EFAP -20) Province_KARS * max(0, EFAP -25) Province_KARS * max(0, FIRSTLIVEWEIGHT-200) FARMERAGE* max(0, EFAP-20) EDUL_Highschool * max(0, PF-10) SOCSEC_unavailable * max(0, EFAP-20) SOCSEC_unavailable * max(0, EFAP-25) SOCSEC_unavailable * max(0, FIRSTLIVEWEIGHT-200) max(0, EFAP -20) * APAP_trade max(0, EFAP -25) * ILF max(0, EFAP -20) * FATPERIOD EFAP* max(0, FIRSTLIVEWEIGHT -200) APAP_home&trade * max(0, FIRSTLIVEWEIGHT-200) ILF * max(0, FIRSTLIVEWEIGHT-200) DLF * max(0, 10- PF) FATPERIOD * max(0, FIRSTLIVEWEIGHT-200) |
253.666268 53.810503 -110.881516 5.429692 62.033653 18.486791 -5.476169 0.216225 -0.371276 -4.225646 -51.314013 2.874303 12.858932 -36.289159 4.762911 0.446050 -3.939783 -107.933446 213.957838 -0.662777 25.099372 -2.207234 -0.509248 0.128674 0.931381 0.043133 0.027965 -0.002299 |
GCV, 494.17; RSq, 0.9963; SDRATIO, 0.0514. PROVINCE, This presents province where farmer lives. A1 (Erzurum, Agri, Igdir and Kars); FARMERAGE, Age of Farmer= (A4); EDUL, Education Level (A5) education level (illiterate, primary_school, secondary_school, high_school and college); SOCSEC, Social Security (A6) available and unavailable. Which aims do you perform animal production? (A9) The aim in performing animal production (APAP ) To meet home’s needs (home), to trade (trade), home and trade (home&trade). Experience of farmer in Animal production (EFAP) =A8. Irrigated land (da) of farmer (ILF) =A19. Dry land (da) of farmer= (DLF)=A20. Pasturage (da) of farmer= PF=A21. A112= Fattening period (day) of male crossbred beef cattle. =FATPERIOD. The first live weight before fattening (kg)=FIRSTLIVEWEIGHT=A113.
However, when EFAP was 20 or earlier years, the MARS model in Table I converted into Table II. Thus, term number of the MARS model was reduced to facilitate the interpretation of the MARS results (Table II).
Table II.- Results of the MARS algorithm for male native beef cattle for EFAP < 20.
|
Basis functions |
Coefficients |
|
Intercept SOCSEC_ unavailable APAP_trade max(0, 10- PF) max(0, PF -10) max(0, 200- FIRSTLIVEWEIGHT) max(0, FIRSTLIVEWEIGHT -200) Province_IGDIR* max(0, FIRSTLIVEWEIGHT-200) Province_KARS * max(0, FIRSTLIVEWEIGHT-200) EDUL_Highschool * max(0, PF-10) SOCSEC_unavailable * max(0, FIRSTLIVEWEIGHT-200) EFAP* max(0, FIRSTLIVEWEIGHT -200) APAP_home&trade * max(0, FIRSTLIVEWEIGHT-200) ILF * max(0, FIRSTLIVEWEIGHT-200) DLF * max(0, 10- PF) FATPERIOD * max(0, FIRSTLIVEWEIGHT-200) |
253.666268 53.810503 -110.881516 -5.476169 0.216225 -0.371276 -4.225646 2.874303 4.762911 -3.939783 -0.662777 0.128674 0.931381 0.043133 0.027965 -0.002299 |
Enterprises performing with an aim of trading animals (APAP_trade) are expected to make a loss of approx. 111 kg in FFW per enterprise. The effect of first weight before fattening on FFW changed from province to province as also seen from 8th and 9th terms of the MARS model in Table II. It was recorded that the effect of first weight before fattening on FFW was influenced by EFAP when the 12th term of the Table II was taken into consideration.
It was reported by Muižniece and Kairiša (2016) that fattening performances of Blonde d’Aquitaine, Hereford, Simmental and crossbred bulls maintained in organic farming system in Latvia was significantly affected by the first weight before fattening, which was in agreement with the results of Aytekin et al. (2017) for young bulls of native, crossbred and cultural breeds. Aytekin et al. (2017) reported that the influence of fattening period on FFW altered based on morphological traits handled, which was in disagreement with those obtained in the present study. Whereas, no influence of fattening period on weight gain was noted by Sarma et al. (2014). Abo Elfadl et al. (2015) found that the effect of fattening period on FFW was non-significant for beef fattening enterprises in Egypt in contrast to those obtained in the current investigation and reported by Aytekin et al. (2017), but Abo Elfadl et al. (2015) found that there is a positive and significant effect of the first weight before fattening on FFW in Egypt in multiple regression analysis technique with a high predictive accuracy of 0.953 R2, which was lower than the present R2 estimate, and also, they did not report the data on a model goodness of fit criterion like SDRATIO.
This difference was attributable to animal age, breed, the first weight before fattening, fattening period, social factors, other biological factors, and managerial conditions, interaction effects of these factors and particularly, to statistical techniques used.
However, it was found in the present study that the influence of the first weight before fattening on FFW varied based on province, social security situation of enterprise, ILF, AFAP and fattening period as a result of more informative outputs obtained in the MARS algorithm. In this respect, it is important to describe common effects of social, economic, and biological factors. In agreement with the results achieved by means of the MARS model, Abo Elfadl et al. (2015) also mentioned that socio-economic and biological factors should be evaluated jointly in order to provide ideal production level of beef cattle. Native breeds that have high adaptability against adverse conditions in their region are important gene sources in a country and should be conserved.
Female native cattle breeds
The results of MARS algorithm applied for female native breeds are presented in Table III. Goodness of fit criteria (0.998 R2 and 0.050 SDRATIO) supported the highest predictive accuracy of the model structured by MARS algorithm. Pearson coefficient of 0.999 displayed the predictive superiority of MARS model (t = 139.5, df = 48, p-value < 2.2e-16). In agreement with the earlier researches, the current SDRATIO value almost reached to 0.05 for ensuring predictive superiority of the fitted MARS model for native female cattle. Thus, trustworthy interpretations could be made by virtue of an outstanding performance in MARS application. In literature, the difference between sexes as an important source of variation was not highlighted by some earlier authors (Demircan et al., 2007; Dadi et al., 2017). Whereas, MARS modeling for each sex was performed in the current survey. As also understood from Table III, it was determined that some significant factors entered into MARS model were province, EDUL, EFAP, ILF, DLF, PF, FATPERIOD, and FIRSTLIVEWEIGHT before fattening, as well as several
Table III.- Results of the MARS algorithm for female native beef cattle.
|
Basis functions |
Coefficients |
|
Intercept Province_KARS EDUL_College max(0, EFAP -25) max(0, 30- EFAP) max(0, EFAP -30) max(0, 30- ILF) max(0, ILF-30) max(0, DLF-50) max(0, 100- DLF) max(0, DLF -100) max(0, 2- PF) max(0, PF -2) max(0, 120- FATPERIOD) max(0, FATPERIOD -120) max(0, 200- FIRSTLIVEWEIGHT) max(0, FIRSTLIVEWEIGHT -200) max(0, FIRSTLIVEWEIGHT -250) Province_KARS* ILF Province_KARS* FATPERIOD Province_ERZURUM * max(0, FIRSTLIVEWEIGHT -200) FARMERAGE * max(0, FATPERIOD -120) EDUL_Secondaryschool * max(0, PF -2) EDUL_Secondaryschool * max(0, FATPERIOD -120) EDUL_College * max(0, FIRSTLIVEWEIGHT -200) SOCSEC_ unavailable * max(0, FATPERIOD -120) max(0, 30- EFAP) * PF EFAP* max(0, 200- FIRSTLIVEWEIGHT) APAP_trade * max(0, 200- FIRSTLIVEWEIGHT) ILF * max(0, 120- FATPERIOD) DLF * max(0, 120- FATPERIOD) DLF * max(0, FATPERIOD -120) max(0, 100- DLF) * FATPERIOD DLF * max(0, FIRSTLIVEWEIGHT -200) PF * max(0, FIRSTLIVEWEIGHT -200) |
658.69906 -5.42734 60.50849 8.16573 -2.21058 -15.89435 -1.96080 -0.03898 -2.46559 -5.82719 3.70978 -102.04745 -3.26919 6.48396 -3.61987 -2.33197 3.01390 -1.55665 -10.24252 0.25759 -1.65964 0.05433 1.18951 0.41847 -2.64804 -0.85960 -0.08546 0.03951 15.34839 -0.04179 -0.05879 0.00068 0.02595 0.00006 -0.03709 |
GCV, 52.950; RSq, 0.998; SDRATIO, 0.050; PROVINCE, This presents province where farmer lives. A1 (Erzurum, Agri, Igdir and Kars); FARMERAGE, Age of Farmer= (A4); EDUL, Education Level (A5) education level (illiterate, primary_school, secondary_school, high_school and college); SOCSEC, Social Security (A6) available and unavailable. Which aims do you perform animal production? (A9) The aim in performing animal production (APAP ) To meet home’s needs (home), to trade (trade), home and trade (home&trade). Experience of farmer in Animal production (EFAP) =A8. Irrigated land (da) of farmer (ILF) =A19. Dry land (da) of farmer= (DLF)=A20. Pasturage (da) of farmer= PF=A21. A100= Fattening period (day) of male crossbred beef cattle =FATPERIOD. The first live weight before fattening (kg)=FIRSTLIVEWEIGHT=A101.
significant interaction effects entered into MARS model were all the term between 19th and 35th terms. As also mentioned above, the first live weight before fattening in the present study was found as a significant source of variation for FFW in native female beef cattle. It could be suggested that the influential factor was interacted with some factors i.e. province, EDUL, APAP, DLF and PF (Table III). These present results were not in line with those reported by Muižniece and Kairiša (2016) and Aytekin et al. (2017), who reported the significant main effect of the first weight before fattening for bulls. The significant interaction effects found here supported the statements of Abo Elfadl et al. (2015), who said that socio-economic and biological factors should be handled together in order to provide ideal production level of beef cattle. The present study revealed the superiority of the MARS modeling with very high predictive accuracy for the data regarding native beef cattle, which is of predominantly importance in socio-economic development (Hicks, 1995).
MARS basic functions and coefficients in Table III were transformed into Table IV in order to make much easier interpretation. In the example provided in Table IV, a prediction equation was developed for province = Iğdır, FATPERIOD= 120 days, EDUL=college, PF=2, EFAP=30, APAP=trade, ILF=30, DLF=100 and SOCSEC=available.
For instance, FFW was predicted as 640.1 kg for FIRSTLIVEWEIGHT= 210 kg (FFW prediction = 636.7567 + (3.01390* 10) –(2.64804*10)+ (0.00006*100*10)-(0.037092 *10) = 640.1 kg).
These differences between our results and the earlier results were ascribable to social factors (educational level, farmer’s age, farmer’s province, farmer’s social security situation etc), biological and economic factors (breed, gender, first live weight before fattening, and fattening period), managerial conditions, interaction effects of these factors and specifically, to statistical techniques employed.
Table IV.- Results of the MARS algorithm for female native beef cattle.
|
Basis functions |
Coefficients |
|
Intercept max(200- FIRSTLIVEWEIGHT) max(FIRSTLIVEWEIGHT -200) max(FIRSTLIVEWEIGHT -250) max(FIRSTLIVEWEIGHT -200) 30* max(200- FIRSTLIVEWEIGHT) max(200- FIRSTLIVEWEIGHT) 100* max(FIRSTLIVEWEIGHT -200) 2 * max(FIRSTLIVEWEIGHT -200) |
636.7567 -2.33197 3.01390 -1.55665 -2.64804 0.03951 15.34839 0.00006 -0.03709 |
GCV, 52.950; RSq, 0.998; SDRATIO, 0.050.
Conclusion
In the current study, we made an examination of describing influential factors on FFW in the native breeds using MARS data mining algorithm with the highest predictive accuracy of nearly 100% of total variability in the FFW. It was found that MARS algorithm with the interaction order of 2 may be a valuable preference on very successfully exhibiting socio-economic (province, FARMERAGE, EDUL, EFAP, SOCSEC, APAP, PF, ILF, DLF) and biological (FIRSTLIVEWEIGHT before fattening, FATPERIOD) factors affecting FFW. In conclusion, we recommended that socio-economic and biological factors influencing FFW in native beef cattle should be handled jointly by applying MARS algorithm, which is specified without any need of distributional assumption on influential factors.
Statement of conflict of interest
Authors have declared no conflict of interest.
References
Abo Elfadl, E.A., Fardos, A.M. and Radwan, H.A.A., 2015. Quantitative methods to determine factors affecting productivity and profitability of beef fattening enterprises in Egypt. Global Vet., 14: 77-82.
Ahmed, K., Tamir, B. and Mengistu, A., 2010. Constraints, opportunities and challenges of cattle fattening practices in urban and peri-urban kebeles of Dessie Town, Ethiopia. J. Fish. Livest. Prod., 4: 203.
Akin, M., Eyduran, E. and Reed, B.M., 2017a. Use of RSM and CHAID data mining algorithm for predicting mineral nutrition of hazelnut. Pl. Cell Tissue Organ Cult., 128: 303-316. https://doi.org/10.1007/s11240-016-1110-6
Akin, M., Eyduran, E. and Reed, B.M., 2017b. Developing of optimal tissue culture medium for Hazelnuts. IX International Congress on Hazelnut, 15-19 August, Atakum, Samsun, Turkey.
Akin, M., Eyduran, E., Niedz, R.P. and Reed, B.M., 2017c. Developing hazelnut tissue culture medium free of ion confounding. Pl. Cell Tiss. Cult., 130: 483-494.
Akin, M., Hand, C., Eyduran, E. and Reed, B.M., 2017d. Predicting minor nutrient requirements of hazelnut shoot cultures using regression trees. Pl. Cell Tiss. Organ Cult., 129: 1-15. https://doi.org/10.1007/s11240-017-1353-x
Ali, M., Eyduran, E., Tariq, M.M., Tirink, C., Abbas, F., Bajwa, M.A., Baloch, M.H., Nizamani, A.H., Waheed, A., Awan, M.A., Shah, S.H., Ahmad, Z. and Jan, S., 2015. Comparison of artificial neural network and decision tree algorithms used for predicting live weight at post weaning period from some biometrical characteristics in Harnai sheep. Pakistan J. Zool., 47: 1579-1585.
Aydin, E., Yeşilyurt, C. and Sakarya, E., 2014. Measuring the performance of cattle fattening enterprises with data envelopment analysis: Comparative analysis of enterprises in the northeast Anatolia region (tra) between the years 2009-2010. J. Facult. Vet. Med. Kafkas Univ., 20: 719-725. https://doi.org/10.9775/kvfd.2014.10958
Aytekin, İ., Eyduran, E., Karadas, K., Akşahan, R. and Keskin, İ., 2017. Prediction of fattening final live weight from some body measurements and fattening period in young bulls of crossbred and exotic breeds using mars data mining algorithm. Pakistan J. Zool., 50: 189-195.
Cozzi, G., 2007. Present situation and future challenges of beef cattle production in Italy and the role of the research. Italian J. Anim. Sci., 6: 389-396.
Dadi, G., Urge, M. and Teklebrhan, T., 2017. Assessment of commercial beef cattle fattening practices and performance in east Shoa zone. Int. J. agric. Sci. Fd. Tech., 3: 067-076.
Demircan, V., Köknaroglu, H. and Yılmaz, H., 2007. Effect of season on beef cattle performance and profitability. Agric. Trop. Et. Subtrop., 40: 19-23.
Hicks, C., 1995. The role of Zambian cattle populations in socio-economic development. Livest. Res. Rural Develop., 7: Article#19. http://www.lrrd.org/lrrd7/2/3.htm
Kornacki, J. and Ćwik, J., 2005. Statystczyn systemy uczqce sie. Wyd. Nauk.-Techn., Warszawa, pp. 90-95.
Kovalchuk, I.Y., Mukhitdinova, Z., Turdiyev, T., Madiyeva, G., Akin, M., Eyduran, E. and Reed, B.M., 2017. Modeling some mineral nutrient requirements for micropropagated wild apricot shoot cultures. Pl. Cell Tiss. Organ Cult., 129: 325-335. https://doi.org/10.1007/s11240-017-1180-0
Kovalchuk, I.Y., Mukhitdinova, Z., Turdiyev, T., Madiyeva, G., Akin, M., Eyduran, E. and Reed, B.M., 2018. Nitrogen ions and nitrogen ion proportions impact the growth of apricot (Prunus armeniaca) shoot cultures. Pl. Cell Tiss. Organ Cult., 133: 263–273. https://doi.org/10.1007/s11240-018-1379-8
Köknaroğlu, H., Loy, D.D., Pas, D.E., Wilson, Hoffman, M.P. and Pas Lawrence, J.D., 2005. Factors affecting beef cattle performance and profitability. Profess. Anim. Scient., 21: 286-296. https://doi.org/10.15232/S1080-7446(15)31220-1
Marle, J.V., 1974. The breeding of beef cattle in South Africa: Past, present and future. S. Afr. I. Anim. Sci., 4: 297-304.
Muižniece, I. and Kairiša, D., 2016. Different beef breed cattle fattening results analysis. Res. Rural Develop., 1: 57-62.
Sarma, P.K., Raha, S.K. and Jørgensen, H., 2014. An economic analysis of beef cattle fattening in selected areas of Pabna and Sirajgonj districts. J. Bangladesh Agric. Univ., 12: 127-134. https://doi.org/10.3329/jbau.v12i1.21402
Tutkun, M., 2017. The red meat production in Turkey. Scient. Pap. Ser D. Anim. Sci., 60: 278-283.
To share on other social networks, click on any share button. What are these?










