Technical Efficiency of Broiler Farms in District Mansehra, Pakistan: A Stochastic Frontier Trans-Log Production Approach
Technical Efficiency of Broiler Farms in District Mansehra, Pakistan: A Stochastic Frontier Trans-Log Production Approach
Ronaq Zaman*, Shahid Ali and Inam Ullah
University of Agriculture, Peshawar, Pakistan.
Abstract | This paper estimates the technical efficiency of broiler farms in district Mansehra, Khyber Pakhtunkhwa, Pakistan. Primary data were collected from 134 respondents using multi-stage sampling technique through well-structure interview schedule. For the estimation of Stochastic frontier tans-log production function, maximum likelihood estimation technique was used. To ensure the abnormality of data set Chow test and Dummy variable test was employed for any possible structure break across the broiler farms. Results indicated that there were significant structural breaks across the sampled farms. Based on these findings three different model was estimated for small, medium and large farms, respectively. The mean calculated technical efficiencies for small, medium and large farms were respectively 0.76, 0.96 and 0.92. This implies that the medium size farms in the study area were the most efficient in resource utilization as compared to small and large size farms whereas the small size farms were the most inefficient in resource allocation. Education has a positive and significant effect on the technical efficiency of small and medium farms. Therefore government should encourage educated people in broiler farming. Broilers farmers also need to be provided with loan facility on easy installments, for a smooth running of broiler farms in future.
Received | December 07, 2016; Accepted | January 15, 2018; Published | February 21, 2018
*Correspondence | Ronaq Zaman, University of Agriculture, Peshawar, Pakistan; Email: [email protected]
Citation | Zaman, R., S. Ali and I. Ullah. 2018. Technical efficiency of broiler farms in District Mansehra, Pakistan: a stochastic frontier trans-log production approach. Sarhad Journal of Agriculture, 34(1): 158-167.
DOI | http://dx.doi.org/10.17582/journal.sja/2018/34.1.158.167
Keywords | Broiler farms, Technical efficiency, Trans-log production function, stochastic frontier analysis, Pakistan
Introduction
Poultry farms are those farms that raise chickens, turkeys, ducks and other birds for production of meat and egg (Hamra, 2010). Mainly chickens are reared with three motives. First they are the cheapest source of income secondly, enrich in amino acid they are good source of protein and third motive is in cultural consideration which people attached to them (Alders et al., 2009). Poultry is one of the blistering and vivacious sector of agricultural industry and play a prominent role in the GDP of Pakistan. After textile it is the second largest segment. The employment opportunities created by this industry is estimated at 1.5 million. Poultry sector share in GDP of Pakistan at factor cost is 1.3% whereas in agriculture sector its contribution is 6.1% and in livestock it is accounted for 10.8%. Out of total country meat consumption 28% came from poultry sector. Currently this industry employed an investment of 200 billion and annually increasing at rate of 10%. The Per capita poultry consumption in Pakistan is increasing at a rate of 4% per annum. Pakistan is still way behind in per capita meat consumption level as recommended by dietary allowance (RDA). Compared to developed countries, where per capita meat consumption is 41 kg per person, Pakistan meat consumption is 17.5 kg per annum. While in developing economies it is 28.4 kg per person (GoP, 2014).
Generally, chickens are reared for three main purpose. Those rear for meat production are broilers, to get new offspring from the production of fertile eggs are breeder and those of table egg producers are known as layer (Ahsan and Masood, 2004). The production of broiler started from the pure strain that make the Great Grand Parents (GGP). Which in turn gave the grandparent and available in Pakistan. From grandparents parent stocks (Breeders) are produced which end up in the final product broiler (SMEDA, 2010).
Pakistan is far behind in broiler production as compared to her regional competitor. This may be due to low productivity and inefficient utilization of resources and poor management. Therefore the measurement of broiler producers’ efficiency is of important concern in developing economies. Moreover efficiency is an important factor of productive growth especially in developing economies where productive resources are meager. The crucial role of efficiency (particularly technical efficiency) in increasing agriculture growth has widely recognized by researcher and policy makers. Indeed, considerable efforts have been devoted to the analysis of farm level efficiency in developing economies in crop sector. Most of the research studies in developing economies were conducted to analyze farm level efficiency. Most of the studies carried out on technical efficiency of broiler farming e.g., Ali et al. (2014) and Afridi (2015), among others, estimated technical efficiency of broiler farms used Stochastic Frontier Cobb Douglas production function. It is important to mention that trans-log production function has not yet been applied in previous studies estimating technical efficiency of broiler farms in Pakistan. This study therefore is an attempt for estimation of technical efficiency of broiler farms employing trans-log production function. Trans log production function is smoother than Cobb Douglas production function as it explains all three stages of production whereas Cobb Douglas production function is homogenous of only degree 1 (Debertin, 2012 and Coelli et al., 2005). Therefore this study employed Trans log production function to estimate and examine the technical efficiency of broiler farms in district Manshera, Pakistan.
Materials and Methods
This study was conducted in Mansehra district. Mansehra is the north eastern district of Khyber Pakhtunkhwa, Pakistan at altitude of 975.36 meters with an average annual population growth rate of 2.4% and literacy rate of 36.3%. It is a large district with a total of 1476 broiler farms approximately (SMEDA, 2009).
In order to collect data from sample respondents a multi-stage technique sampling was used. In stage-first, District Manshera was purposively selected because it is one of the larger producer of broiler in Khyber Pakhtunkhwa. In stage second areas with maximum number of broiler producing farms were purposively selected. And finally in the third stage, 140 open shed broiler farms were randomly selected through proportional allocation sampling technique using the following formula (Cochran, 1977):
ni = n (Ni/N)……….(1)
Where;
ni: Sample of broiler farms to be taken from ith village; n: Total size of sample; Ni: Total broiler farms in ith village; N: Total population of broiler farmers in the study area.
Analytical framework
Measuring farm level efficiency is an essential question in emerging agricultural countries (Parikh et al., 1995). Efficiency of farmers is of high concern to economist dealing with the problem of increasing production with given farms resources using least cost combination (Belbase and Richard, 1985). The first hall marker in measuring efficiency was Farrell (1957) when he published a seminal paper in 1957 (Alrwis and Francis, 2003). Farrell defined efficiency as “the ability to produce maximum output at least cost combination” and further sub-divided it into technical, allocative and economic efficiency. “Technical efficiency is the measurement of capacity of a farm in obtaining maximum quantity of output from available set of input” whereas “the ability of farm to measure a level to equate price to it marginal value product is allocate efficiency” and finally economic efficiency is achieved “when a farm combine resources in best cost combination to produce maximum level of output (TE) and at the same time ensure to obtain largest possible revenue (AE)” (Mahjoor, 2013).
Model specification
In economics producer performance and evaluation of productivity has become an important subject to researchers and policy makers. Broiler production therefore involves this evaluation for measurement and analysis of efficiency (Yin, 1998). For measurement of efficiency analysis two main techniques are used. One of them is Data Envelopment Approach (DEA) and Free Disposal Hull (FDH), non-parametric in nature and use linear programming. These two differ from each other in the way that DEA was developed by Farrell (1957) and improved into estimation technique by Charnes et al. (1978) whereas FDH method was introduced by Deprine et al. (1984). The former method is mainly criticized due to following limitations:
- 1. For testing hypothesis it lacks in statistical procedure.
- 2. It has made no assumption for error term which open window for inefficiency.
- 3. Very sensitive to the most deviated and outlier values (Ali et al., 2014).
Second method for measuring efficiency is parametric in nature and assume a specific functional form for production frontier. It is again of four types: 1. deterministic production frontier; 2. statistical production function frontier; 3. statistical production function frontier that consider gamma-distribution; and 4. stochastic production frontier with a composed error-structure. The first three methods are not considered as efficiency measure because their entire deviation from frontier contributes to inefficiency (deterministic) while the fourth one has contributed only a part to deviation from the frontier to inefficiency (Bravo and Reiger, 1990). The first three deterministic models are being criticized for not taking account for error term and other noises along frontier (Coelli et al., 1998).
This study used stochastic production frontier approach to measure the technical efficiency of broiler producers because stochastic frontiers were widely used in developing economies to analysis the efficiency, particularly in agriculture. The main advantages of stochastic frontier approach are that it deal with stochastic noise, hypotheses testing for concern production technology and also data and information regarding small farmers are usually incorrect because they do not have rationalized data. So it is the main strength of stochastic frontier technique to instantaneously take up random-error term and inefficiency factors specific to every farmer to estimate frontier function.
Stochastic frontier production function
The idea of stochastic frontier was autonomously presented by Aigner, Aigner and Lovell (1977), Meeusen and Vander Broek (1977) in the form as fallow. (Collei et al., 1998).
In qi = X´i β + vi - µi ………..(2)
where i = 1, 2, ……., n
qi: Output of the ith firm; X’i : K x 1 vector containing the logarithms of inputs; β: Unknown parameters to be estimated, µi: Non-negative random variable associated with technical inefficiency; vi : Error term or statistical noise.
Yi = f (Xi, β) exp (vi - µi)…….(3)
where i = 1, 2, 3,….., n
Yi : Output obtained from ith farm; Xi: Vector of input used by ith farm; β: Unknown parameter to be estimated; f ( ) represent an appropriate function form (e. g Cobb-Douglas, trans-log, etc). The term vi stand for a symmetry error, which account for the random variation in production due to factors which are beyond the control of farm producer for example disease break, weather and measurement error etc. The random error term Vi is assumed by Aigner et a.l (1977) to be independently and identically distributed as N (0, σ2v) independent of µis which are assume to be non-negative and in the control of the farmer, associated with technical inefficiency of the poultry farm, truncation of N (0, σ2v) distribution i. e half normal distribution or have exponential distribution which ranges from 0 to 1.
Technical efficiency
The technical efficiency can be calculated as.
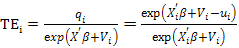
TEi = exp (-µi) = Yi/Yi*……(4)
Takes value between zero and one; 1 mean technically efficient firm and 0 shows inefficiency (Coelli et al. 1998).
Econometric model
In order to estimate the technical efficiency of broiler producing farmers in district Mansehra, both Cobb Douglas and trans-log production function were simultaneously estimated to dig out which production function best suit the pure nature of data. Results from both models inferred that trans-log production is more powerful as compared to Cobb Douglas production function to explain the exact nature of data set. The econometric model used in this study to estimate the technical efficiency of broiler producers was a modified form of trans-log production function with incorporated input as follows: (Equation 5)
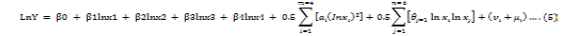
Where j = 1, 2….. n
Y: Production of broiler per shed in kilograms; X1: Represent feed intake per shed in kilograms; X2: Number of chicks per shed; X3: Vaccination in cc (cubic centimeter) per shed and finally; X4: Labor in men days; vi: Natural error term; μi: shows technical inefficiency error terms; β, α and θ: Parameters to be estimated.
After the estimation of the above given model and model adequacy tests the data set were founded skewed to left tail. This study used demean to confirm the skewed nature of data and to see variation amongst the variables. After thoughtful and in depth investigation of data set gave clear supposition for structural break. This study then tested the above model for structural break across the broiler farms to find out whether the data on broiler farms should be regressed on one data set or different model should be estimated for different data sets. Gujarati (2004) outline the procedure how to test the structural differences across models through estimation of Chow’s F-value as:
F=(RSSr – RSSur) / k / (RSSur) / (n1+n2-2k)…..(6)
Where
RSSr: Restricted residual sum of squares obtained from pool data; RSSur: Unrestricted residual sum of squares obtained from RSS1 and RSS2; n1 and n2: Respectively the number of observation in two sub sets; K: Number of parameters to be estimated. Chow’s F ratio follows F distribution with degree of freedom (n1+ n2-2k). If Chow’s F value is statistically significant it would suggest that there is structural break across the regions. But it is important to mention that Chow’s test only tell us whether the two regression are different, without telling us whether the difference is on account of intercepts, or slopes, or both. Gujarati (2004) for this purpose suggested the dummy variable alternative to the Chow test. The source of differences, if any, can be pinned down by pooling all the observations (134 in all, after excluding out the outlier from the data set). Chow test with dummy variable were tested at different points in order to seek out the actual point of breaks using E-views statistical software package. From the projected results it was concluded that Chow test with dummy as a variable was statistically significant at sample number 81 with P-value (0.01), where D = 1 if farm size was 4000 or greater and D = 0 if otherwise. When two sub data sets were separately regressed the data set with 81 observations again showed clear concerned for structural break and was significant with P-value (0.013) at sample number 36, where D = 1 if farm size was 3000 or above and D = 0 if otherwise. In addition three dummy variable test with output, variable cost and technical efficiency were also performed for further confirmation of structural break and all these test were statistically significant.
Determinants of technical inefficiency of broiler farms
To find out factors effecting the technical efficiency of broiler producers, the following model was jointly estimated with the stochastic frontier model in a single stage (Coelli et al. 1998). The model is given as follows:
μi = δ0 + δ1 Z1 + δ2 Z2 + δ3 Z3 + δ4 Z4 + δ5 Z5 + δ6 Z6 + δ7 Z7 + δ8 Z8 …….. (7)
Where
μi: Technical inefficiency error term; Z1: Farmer age in years; Z2 : Education of farmer in years; Z3 : Average vaccination cost (Dummy); Z4: Experience of broiler farmers in years; Z5: Main occupation of farmer (Dummy); Z6: Distance from market (Dummy); Z7: Ownership of farm (Dummy); Z8 : Live ratio; δi : Unknown parameters to be estimated whereas ωi is random error term.
Estimation of technical inefficiency of individual broiler farm
For the estimation of technical inefficiency of individual broiler farm, the following formula was used.
TEi =Yi/Yi* …………. (8)
TIi=1-TEi ...................(9)
Where
Yi: Observed output of ith farm; Yi*: Frontiers output of ith farm that can be achieved.
Table 1: Farms distribution after structural break based upon chow test.
| Farms | Range/ Birds per shed | Frequency |
| Small | 1500-2900 | 36 |
| Medium | 3000-3900 | 45 |
| Large | 4000-7000 |
35 |
Source: Estimated from survey data, 2016.
Results and Discussion
Based upon the findings of chow test with confirmation from dummy variable test the original sample was split in to small medium and large size farms as shown in Table 1. Where a break at observation 36, ranging from 1500 to 2900 birds per shed, shows the sample size of small broiler farms. A structure break at sample observation 81 indicating a sample size of 45 broiler farms of medium size having capacity of 3000-3900 birds per shed. Similarly the sample size for large size farms is 45 possessing a capacity of 4000-7000 chickens per shed Table 2 represent the summary-statistics of the variable used in prediction of stochastic frontier trans-log production function and values in parenthesis shows the standard deviation. From the table the average production of broiler per shed in small farms was 3,053.26 kg with standard deviation of 589.70. Which shows the average variability in the small size broiler farms. The average value of feed consumed per shed in small farms was 6,552.77 Kg with standard deviation of 1,385.12. The average number of broiler reared per shed in small size farms was 2,113. Whereas the variability shown by the standard deviation in small farms was 357.89. On average 305.55 CC of vaccination was given to the broiler in small farms and it standard deviation was recorded 104.10 per small shed. The mean of labor in man days was found 40.63 days with standard deviation of 1.47.
Similarly, the average output in kilogram generated in medium size farms was 4,747.84 Kg with standard deviation of 674.56 Kg. On average consumed 10,124.44 Kg of feed and it stander deviation was 1,178.53 Kg. The mean of number of broiler reared in medium size farms was 3220 while it calculated standard deviation was 287.30. The variation in value of vaccine per shed of medium size farms was calculated through standard deviation, which was 144.42 CC and its mean value is 492.17 CC. Medium size farms labor, on average took 41.31 man days to look after the birds and manage other farm activities with sander deviation of 1.53 men days.
Table 2: Summary statistics of variables used in stochastic frontier analysis.
| Variables | Units | Small | Medium | Large |
| Mean | Mean | Mean | Mean | |
| Output | Kg |
3,053.26 (589.70) |
4,747.84 (674.56) |
7,943.74 (2,283.23) |
| Feed | Kg |
6,552.77 (1,385.12) |
10,124.44 (1,178.53) |
15,948.11 (3,453.45) |
| Day old chicks | No |
2,113 (357.89) |
3,220.00 (287.30) |
5,084.90 (978.10) |
| Vaccination | Cc |
305.55 (104.10) |
492.17 (144.42) |
921.24 (325.49) |
| Labor | M Days |
40.63 (1.47) |
41.31 (1.53) |
41.71 (1.66) |
| Age | Years |
21 (8.09) |
35.06 (8.94) |
38.73 (9.70) |
| Education |
Years |
11.66 (3.49) |
12.15 (2.50) |
10.73 (5.05) |
| Vaccination cost | Dummy |
0.33 (0.47) |
0.46 (0.50) |
0.50 (0.50) |
| Experience | Years |
9.55 (6.87) |
12.04 (7.88) |
15.58 (10.01) |
| M occupation | Dummy |
0.91 (0.28) |
1 (0) |
0.92 (0.26) |
| Distance from market | Dummy |
0.25 (0.43) |
0.2 (0.40) |
0.15 (0.26) |
| Ownership | Dummy |
0.91 (0.28) |
0.93 (0.25) |
0.83 (0.37) |
| Live ratio | No |
189.19 (71.99) |
282.88 (184.16) |
419.01 (268.42) |
Source: Estimated from survey data, 2016.
In same way the average output of large size farms was 7,943.74 Kg and its standard deviation was 2,283.23 Kg. Per shed feed consumption was found on average 15,948.11 Kg. Mean day old chicks was 5,084.90 with standard deviation of 978.10. The average vaccination was 921.24 CC with standard deviation of 325.49 CC. The average value of labor in man days was found to be 41.71 and variation in large farm man days was 1.66. The lower part of table shows the summary statistics of inefficiency variables used in stochastic frontier analysis of broiler production in study area.
Table 3 explains the estimated coefficients of stochastic frontier Trans-log production function of small, medium and large size broiler farms. The estimated
Table 3: Maximum likelihood estimates of the stochastic frontier production function of broiler farmers.
| Farm size | Small size farms | Medium size farms | Large size farms | ||||||||
| Variables | Parameters | Cff | SE | TR | Cff | SE | TR | Cff | SE | TR | |
| Constant |
β0 |
15.28 | 116.5 | 1.31 | -239.56** | 0.987 | -242.57 | 177.25** | 6.261 | 28.30 | |
|
Lnx1 (Feed) |
β1 |
-45.80* | 18.58 | -2.46 | 77.16** | 0.764 | 100.98 | -40.45** | 8.763 |
-4.62 |
|
|
Lnx2 ( DOC) |
β2 |
22.60 | 14.15 | 1.60 | -94.03** | 0.780 | -120.52 | 38.07** | 4.263 | 8.93 | |
|
Lnx3 Vaccination) |
β3 |
7.67* | 3.591 | 2.14 | -15.26** | 0.822 | -18.56 | -0.55 | 3.378 | -0.16 | |
|
Lnx4 (Labor) |
β4 |
-30.25 | 42.63 | -0.71 | 168.01** | 0.948 | 177.05 | -74.06** | 8.147 | -9.09 | |
|
0.5 (lnx1)2 |
α1 |
0.08 |
0.232 |
0.37 | 7.80** | 0.428 | 18.19 | -0.01 | 0.643 | -0.01 | |
|
0.5 (lnx2)2 |
α2 |
-2.11* | 1.151 | -1.83 | 8.43** | 0.570 | 147.74 | 11.48** | 2.236 | 5.14 | |
|
0.5 (lnx3)2 |
α3 |
0.54* | 0.267 | 2.04 | -0.80** | 0.217 | -3.69 | -0.07 | 0.259 | -0.27 | |
|
0.5 (lnx4)2 |
α4 |
-3.49 | 9.221 | -0.37 | -36.82** | 0.651 | -56.49 | 12.2** | 3.685 | 3.30 | |
|
0.5 lnx1lnx2 |
θ1 |
2.63 | 1.918 | 1.37 | -16.47** | 0.579 | -28.44 | -10.99** | 3.011 | -3.65 | |
|
0.5 lnx1lnx3 |
θ2 |
-0.92 | 1.173 | -0.79 | 3.90** | 0.603 | 6.46 | 2.51 | 2.061 | 1.22 | |
|
0.5 lnx1lnx4 |
θ3 |
0.20* | 9.319 | 2.19 | -50.73** | 0.547 | -92.74 | 42.35** | 2.566 | 16.49 | |
|
0.5 lnx2lnx3 |
θ4 |
0.09 | 0.882 | 0.11 | 1.73* | 0.776 | 2.23 | -2.04 | 1.920 | -1.06 | |
|
0.5 lnx2lnx4 |
θ5 |
-9.36 | 7.924 | -1.18 | 52.44** | 0.444 | 118.08 | -40.19** | 2.321 | -17.31 | |
|
0.5 lnx3lnx4 |
θ6 |
-3.84* | 1.830 | -2.10 | -2.56** | 0.226 | -11.29 | -1.30 | 1.801 | -0.72 | |
| Technical Inefficiency effects model | |||||||||||
| Constant |
δ0 |
0.4707* | 0.220 |
2.1335 |
0.0921 | 0.711 | 0.1296 | -3.1467* | 1.709 | -1.8407 | |
| Age |
δ1 |
-0.0036 | 0.002 | -0.1857 | -0.0018 | 0.003 | -0.7012 | 0.0311 | 0.024 | 1.2669 | |
| Education |
δ2 |
-0.0078** | 0.003 | -3.1132 | -0.0101* | 0.004 | -2.2697 | 0.0522* | 0.026 | 1.9788 | |
| Vaccination cost |
δ3 |
-0.0163 | 0.041 | -0.3928 | 0.0337 | 0.033 | 0.9933 | -0.7025* | 0.361 | -1.9411 | |
| Experience |
δ4 |
0.0039 | 0.002 |
1.7305 |
0.0031 | 0.003 | 1.0885 | -0.0324 | 0.021 | -1.4635 | |
| Main occupation |
δ5 |
-0.0866* | 0.035 | -2.4541 | 0.0921 | 0.711 | 0.1296 | 0.4119 | 0.235 | 1.7485 | |
| Dist frm market |
δ6 |
-0.0495* | 0.018 | -2.4376 | 0.0165 | 0.029 | 0.5701 | 0.5374 | 0.309 | 1.7346 | |
| Ownership f farm |
δ7 |
-0.1089* | 0.036 | -2.9597 | -0.0458 | 0.047 | -0.9649 | -0.7644* | 0.395 | -1.9306 | |
| Live ratio |
δ8 |
0.0035** | 0.000 |
2.8657 |
0.0008 | 0.000 | 1.2577 | 0.0009* | 0.000 | 2.3082 | |
|
Sigma u2 |
σ2u |
0.0006 | 0.0001 | 0.1563 | |||||||
|
Sigma v2 |
σv2 |
0.0001 | 0.0287 | 0.0011 | |||||||
|
Sigma2 |
σ2 |
0.0007** | 0.000 | 4.2620 | 0.0033** | 0.000 | 4.4515 | 0.1575 | 0.073 | 2.1422* | |
|
Gama (σ2u/σ2) |
Y | 0.8571 | 0.633 | 1.4336 | 0.0294 | 0.165 | 0.1937 | 0.9930 | 0.005 | 188.04** | |
| Mean TE |
Xmean |
0.7605 | 0.9634 | 0.9222 | |||||||
| Minimum TE |
Xmini |
0.8834 | 0.9973 | 0.9901 | |||||||
| Maximum TE |
Xmaxi |
0.6645 | 0.8748 | 0.6682 | |||||||
Source: Estimated from survey data, 2016. *And ** shows significance at 05% and 01 % respectively.
coefficients of small, medium and large size farms forinput variable X1 (feed) were statistically significant. It is negative in small and large size farms. Dziwrnu et al. (2013) and Adepoju (2008) also experienced the negative effect of feed on output. Whereas in medium size farms it is with positive sign which shows the additional production capacity of medium size farms producer as recorded by Adedeji (2013), Ohajianya (2013) and Ezeh et al. (2012).
The predicted coefficient of X2 (day old chick) is insignificant for small size farms it might be due to the over population in sheds. It is negatively signed and statistically significant for medium size farms. According to Ali et al. (2014) and Afridi (2015) this negative effect is due to the low stander of day old checks being reared by medium size producer in lure of profit which results in under production at increasing cost. Similarly it carried positive sign and significant at critical value for large size farms which is in line with the findings of Ohajianya et al. (2013), Ezeh et al. (2012), Oleke and Isinnika (2011) and Udoh (2009).
The coefficient of X3 (vaccination) is statistically significant having positive sign for small size farms. The small producer being prudent of his cost constraint tend to use good quality limited vaccination which helps them up left the output level. Whereas for medium size farms the coefficient is negative indicating the use of low quality minimum price vaccination to cope with their increasing cost. Dziwrnu et al. (2013) also reported negative sign of vaccination in their study.
The estimated coefficient of X4 (labor) is statistically significant at 0.05 level of significance for medium size farms, similar to the findings of Ali et al. (2014), Ezeh et al. (2012) and Afridi (2015).
Whereas the estimated coefficient of labor is significant and carrying negative sign for large size farms. These findings are in coherence with Tuffor (2014), Ezeh (2012) and Chukwuji (2006).
The lower part of Table 3 shows the estimates of technical inefficiency models. Age is statistically insignificant in all three categories of farms. The coefficients of education are statistically significant for all sizes of farms. Negative for small and medium size farms which means that technical inefficiency decrease with increase in education. Okon (2010) and Udoh (2009) experience similar results. Positive coefficient of education for large size farms signifying inefficiency. The average vaccination cost (Dummy) in large size farms was significant with negative sign specifying the fact of increasing efficiency with decrease in average cost of production. Experience in broiler farming is significant in medium size farms similar results are also obtained by Tuffor (2014), Adedeji (2013), Tosadee (2012) and Ebong (2009). The coefficient of main occupation (Dummy) is significant with negative sign for small farms which shows that farms rearing broiler, as their main profession, are technically more efficient. It is in contrast to the findings of Yusuf (2007). Distance from market (Dummy) is significant for small broiler farms and the negative sign implementing the fact of increasing efficiency for farms nearer to market as reported Oleke and Issinika (2011). The predicted coefficients of ownership (Dummy) is significant for small farms with negative signs. Indicating that farms owned by sole-proprietors are technically more efficient than those owned otherwise. These results are in agreement with the findings of Tuffour (2014). The estimated coefficients of live ratio is positive for small and large farms counted to inefficiencies in these farms.
Technical efficiency frequency distribution of broiler farmers
Table 4 describes the mean technical efficiencies of small, medium and large farms farmers/producers in study area. They were respectively 0.7605, 0.9634 and 0.9222 and falling in groups with maximum frequency distribution.
Table 4: Frequency distribution of small, medium and large broiler farmers.
| Small size farms | ||
| TE class interval | Frequency | Percentage |
| 0.664-0.744 | 14 | 38.89 |
| 0.744-0.824 | 20 | 55.56 |
| 0.824-0.904 | 2 | 5.56 |
| 36 | 100.00 | |
| Medium size farms | ||
| 0.8748-0.9148 | 4 | 8.89 |
| 0.9148-0.9548 | 11 | 24.44 |
| 0.9548-0.9948 | 24 | 53.33 |
| 0.9948-1.0348 | 6 | 13.33 |
| 45 | 100.00 | |
| Large size farms | ||
| 0.6682-0.7482 | 2 | 3.77 |
| 0.7482-0.8282 | 2 | 3.77 |
| 0.8282-0.9082 | 6 | 11.32 |
| 0.9082-0.9882 | 42 | 79.25 |
| 0.9882-1.0682 | 1 | 1.89 |
| 53 |
100.00 |
|
Source: Estimated from survey data, 2016.
Table 5: Overall technical efficiency of broiler farms.
| Farms | Mean | Mini | Maxi |
| Small | 0.7605 | 0.6645 | 0.8834 |
| Medium | 0.9634 | 0.8748 | 0.9973 |
| Large | 0.9222 | 0.6682 | 0.9901 |
| Weighted average | 0.8925 | 0.7365 | 0.9638 |
Source: Estimated from survey data, 2016.
Overall technical efficiency of broiler farms
Table 5 shows the mean, maximum and minimum efficiencies of small, medium and large farms in column second, third and fourth, respectively. The weighted average values in row five minimum technical efficiency (0.7365), maximum technical efficiency (0.9638) and mean technical efficiency (0.8925) show the overall figures for all farms combined, which is the original sample size (116).
Conclusions and Recommendations
The estimated gamma values for small size farms was 0.8571 whereas for medium farms it was 0.0294 while it was 0.9930 for large farms. These estimated values shows the variation in broiler production due to inefficiency factors. The mean technical efficiencies were 0.75 (small), 0.9659 (medium) and 0.9222 (large). The overall mean technical efficiency was 0.8925 with 0.7365 as minimum and 0.9638 as maximum indicating that, if the broiler farmer efficiently use the current available farm resources he can reduce his cost by 10.75% and increase production. Similarly the most inefficient farmer can save on cost if he increases his production by 26.35%. Results indicated that medium size farms were technically more efficient as compared to small and large size farms. Therefore, Livestock department needs to educate and encourage the farmers to establish medium size farms for enhancing broiler production in the province in particular and in country in general. Education has positive and significant effect on technical efficiency of small and medium farms. Therefore, government needs to encourage and engage educated people in broiler farming. During interview, sampled respondents were complaining about the quality of vaccines and medicines. The government, therefore, needs to establish laboratory to check the quality of vaccines and medicines. In case of losses, broilers farmers needs to be provided with loan facility on easy installments, for smooth running of broiler farms in future.
Author’s Contribution
Data used in this paper is pure, collected by the researcher from the farmers during field survey through well designed interview schedule. Ronaq zaman is the principle author who conducted the most of the research and wrote the paper, having decided what to include. Shahid Ali supervises the data generation and analysis and the proper presentation and interpretation of the results. Inam Ullah is a Ph.D. scholar who facilitated the principle author in references formation and paper format.
References
Afridi, M.A.Y. 2015. Estimation of technical efficiency of broiler farms in District Peshawar, Pakistan. M. Sc. (Honors) thesis, Department of Agriculture & Applied Economics, The University of Agriculture, Peshawar-Pakistan.
Adedeji, I.A., K.M. Adelalu, S.I. Osunjimi and A.O. Otekunrin. 2013. Application of stochastic production frontier in the estimation of technical efficiency of Poultry Egg. World J. Agric. Res. 1(6): 119-123.
Adegbite, D.A., O.L. Afolabi, O.F. Ashaolu and S.O. Akinbode. 2014. Non parametric Estimation of Production Efficiency of Poultry Egg Farming in Ogun State, Nigeria. Am. J. Exp. Agric. 4(14): 1668-1679. https://doi.org/10.9734/AJEA/2014/10611
Adepoju, A.A. 2008. Technical efficiency of egg production in Osun State. Int. J. Agric. Econom. Rural Dev. 7(16): 1536-1540.
Ahsan and Masood. 2004. Poultry Farming in Pakistan, Chapter. 01: 1-7.
Aigner, D.J., C.A.K. Lovell and P. Schmidt. 1977. Formulation and estimation of stochastic frontier production function models. J. Econom. 6: 21-37. https://doi.org/10.1016/0304-4076(77)90052-5
Akhter, S. and M.H.A. Rashid. 2008. Comparative efficiency analysis of broiler farming under Aftab Bahumukhi farm limited supervision and farmers’ own management. Progrss. Agric. 19(2): 195-204.
Alders, R. 2004. Poultry for profit and pleasure. FAO Diversification Booklet 3. Rome. www.fao.org
Alders, R.G. and R.A.E. Pym. 2009. Village Poultry: Still Important to Millions, Eight Thousand Years after Domestication. World’s Poult. Sci. J. 5: 181. https://doi.org/10.1017/S0043933909000117
Ali, S., S. Ali and B. Raiz. 2014. Estimation of Technical efficiency of broiler farming in Punjab, Pakistan. J. Econom. Sustain. Dev. 5(7): 2222-2855.
Alrwis, K.N. and E. Francis. 2003. Technical efficiency of broiler farms in central region of Saudi Arabia: Stochastic Frontier Approach. Agricultural Research Center King Saud University, 5-34.
Belbase, K. and G. Richard. 1985. Technical efficiency in Nepalese agriculture. J. Dev. Areas. 19: 515-26.
Bravo-Ureta, B.E. and L. Rieger. 1990. Alternative production frontier methodologies and dairy farm efficiencies. J. Agric. Econom. 14: 215-26. https://doi.org/10.1111/j.1477-9552.1990.tb00637.x
Chukwuji, C.O., O. E. Inoni., O.D. Ogisi and W.J. Oyaide. 2006. A quantitative determination of allocative efficiency in broiler production in Delta State, Nigeria. Agric. Conspectus Sci. 71(1): 21-26.
Cochran, W.G. 1977. Sampling Techniques, 3rd edition. John Wiley and Sons, New York. pp. 37-45.
Coelli, T.J., D.S.P. Rao and G.E. Battese. 1998. An introduction to efficiency and productivity analysis kluwer academic publishers, London, UK. https://doi.org/10.1007/978-1-4615-5493-6
Debertin, D.L. 2012. Agriculture production economics. 2nd Revised Edition. Macmillan publishing company, New York.
Deprins, D., L. Simar and H. Tulkens. 1984. Measuring labor efficiency in post offices. In: pp. 243–67, eds. M. Marchand, P. Pestieau and H. Tulkens, The Performance of Public Enterprises: Concepts and Measurements. Amsterdam: North-Holland.
Dziwrnu, R.K., W. Seini, D.B. Sprong, G.T-M. Kwadzo and J.K. Kuwornu.. 2013. Does scale matter in profitability of small scale broiler agribusiness production in Gaza. A trans-log profit function. Int. J. Agric. Sustain. Dev. 4(20): 2222-1700.
Ebong, V.O., U.S. Okoro and E.O. Effiong. 2009. Determinants of technical efficiency urban ferming in uyo metropolis of Akwa Ibom State, Nigeria. J. Agric. Soc. Sci. 5(3): 89-92.
Ezeh, C.I., C.O. Anyiro and J.A. Chukwuaba. 2012. Technical efficiency in poultry broiler production in Umuahia Capital Territory of Abia State, Nigeria. Greener J. Agric. Sci. 2(1): 001-007.
Farrel, M.J. 1957. The measurement of production efficiency. J. Royal Stat. Soc. 120(3): 253-290.
GoP. 2014. Economic Survey of Pakistan, 2012-13. Agriculture, poultry. www. finance.gov.pk/survey_12-13
Gujrati, D.N. and D.C. Porter. 2004. Basic econometrics, 5th Edition. McGraw Hill Inc., New York.
Hamra, F.C. 2010. An assessment of potential profitability of poultry farms: A broiler farm feasibility case study. The University of Tennessee Martin.
Ike, P.C. 2011. Resource use and Technical efficiency of small scale poultry farmers in Enugu State, Nigeria: A stochastic frontier approach. Int. J. Poult. Sci. 10(11): 895-98. https://doi.org/10.3923/ijps.2011.895.898
Mahjoor, A.A. 2013. Technical, allocate and economic efficiencies of broiler farms in Fars Province, Iran: Data Envelopment Analysis (DEA) approach. World Appl. Sci. J. 21(10): 1427-1435.
Meeusen, W. and V. Breock. 1977. Efficiency estimation from Cobb-Douglas production functions with composed error. Int. Econ. Rev. 18(2): 435-444.
Ohajianya, D.O., P.N. Onu, J.N. Ugwu, M.N. Osuji., I.U. Nwaiwu, J.S. Orebiyi, C.C. Godson-Ibeji and C.O. Enyia. 2013. Technical efficiency of table egg producer in Imo State, Nigeria. Asia. J. Agric. Ext., Econom. Sociol. 2(2): 118-127.
Ojo, S.. 2003. Productivity and technical efficiency of poultry egg production in Nigeria. Int. J. Poult. Sci. 2(6): 459-464. https://doi.org/10.3923/ijps.2003.459.464
Okon, U.E., A.A. Enete and N.E. Bassey. 2010. Technical efficiency and its determinants in garden egg (Solanum Spp) production in Uyo Metropolis, Akwa Ibom State, Nigeria. Field Actions Science Report.
Oleke, J.M and A.C. Isinikaka. 2011. Assessing the technical efficiency of commercial edgg production in tanzania for improve livelihood. J. Dev. Agric. Econom. 3(8): 343-352.
Omar, M.A.E. 2014. Technical and economic efficiency for broiler farms in Egypt, application of data envelopment analysis (DEA). Glob. Vet. 12(5): 588-593.
Parikh, A., F. Ali and M.K. Shah. 1995. Measurement of economic efficiency in Pakistani Agriculture. Am. J. Agric. Econom. 77: 675 – 85. https://doi.org/10.2307/1243234
SMEDA. 2010. Small and Medium enterprise development authority ministry of industries and production, Government of Pakistan. Pre-feasibility Broiler Farming.
SMEDA. 2009. Small and medium enterprise development authority ministry of industries and production, Government of Pakistan.
Tosadee, A., H.K. Ngamsomsuk and K.Yamauchi. 2012. Technical Efficiency in Broiler Farming in Thailand: Data Envelopment Approach (DEA). 5(8): 34-38.
Tuffour, M. and B.A. Oppong. 2014. Profit efficiency in broiler production: Evidence from greater Accra region of Gana. Int. J. Food Agric. 2(1): 23-32.
Udoh, E.J. and N.A. Etim. 2009. Measurement of Farm level efficiency of broiler production in Uyo, Akwa Ibam State, Nigeria. World J. Agric. Sci. 5(S): 832-836.
Yin, R. 1998. DEA: A new methodology for evaluating the performance afforest products producers. Forest Prod. J. 48: 29-34.
Yususf. S.A. and O. Malomo. 2007. Technical efficiency of poultry production in Ogun State: Data Envelopment Analysis (DEA) Approach. Int. J. Poult. Sci. 6(9): 622-629. https://doi.org/10.3923/ijps.2007.622.629
To share on other social networks, click on any share button. What are these?








